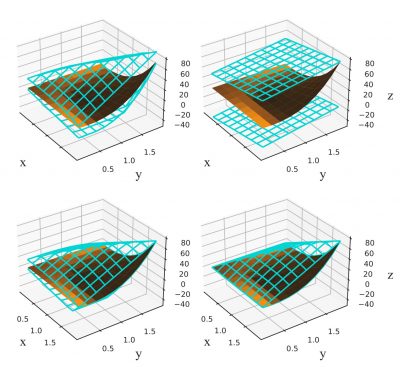
Professor Matthew Stuber, PhD and Dr. Matthew Wilhelm's most recent publication presents new and improved methods for generating convex and concave relaxations of composite bilinear forms. They establish the theoretical framework to generate tighter McCormick-based relaxations in reduced space when intermediate bilinear terms have known convex or concave relaxations. These developments translate into significant speedups when solving deterministic global optimization problems involving these ubiquitous mathematical terms. To read the full publication, click here.